Question

The sides of a triangle are 68, 61, and 46. Use the Pythagorean Theorem to determine if the triangle is right, acute, or obtuse.

Answer 1

Answer: Acute

Explanation:

The Pythagorean Theorem is
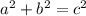`a^2+b^2=c^2`. A and b are legs while c is hypotenuse. Hypotenuse is also the longest side. Let's plug them in and see if they are equal to each other.

`46^2+61^2=68^2` [exponent]

`2116+3721=4624` [add]

`5837\\eq4624`

Since they are not equal, then it is not a right triangle.

To tell is a triangle is acute, if the sum of the two shorter sides squared is greater than the longest side squared, then the triangle is acute.

At the end of the Pythagorean Theorem, we got 5837≠4624. 5837>4624, so that tells us that the triangle is acute.