First, we need to find the midpoint of the segment using the formula;
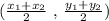
so that we have;
x₁= 5 y₁ = 4 x₂ = -7 y₂=-8
(5-7 /2 , 4-8 /2 )
(-2/2 , -4/2)
(-1 , -2)
(-1 ,-2) gives the midpoint. This is where the segment is bisected.
Next is to determine the slope that is perpendicular to the existing segment
So we will use the slope formula to determine that;
slope(m) =
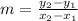
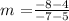
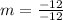
m = 1
The slope of a permendicular lines are opposite and reciprocal
Hence the slope of the perpendicular line is -1
We know that the perpendicular line passes through the point (-1 , -2) and has a slope of -1
Hence, we can now find our intercept using;
y= mx + b
-1 = (-1)(-2) + b
-1 = 2+b
subtract 2 from both-side of the equation
-1-2 = b
b =-3
Therefore the equation of the perpendicula bisector is;
y = -x -3