Question

For the three-part question that follows, provide your answer to each question in the given workspace. Identify each part with a coordinating response. Be sure to clearly label each part of your response as Part A, Part B, and Part C.

Use the image below for Part A, Part B, and Part C.

Two triangles: GHI and JKL
Both have one similar angle but different side lengths

Part A: Sharon says the triangles above are similar using the AA Postulate. Is she correct?

Part B: Explain the answer from Part A.

Part C: If HI=7, find KL. Show your work.



Please Help!

Answer 1

see explanation

Explanation:

A

for the triangles to be similar by the AA postulate then 2 angles in both triangles must be congruent.

In this case we are only given 1 pair of congruent angles.

Thus not able to say similar by AA postulate, therefore Sharon is incorrect in her assumption.

B

the sides are of different lengths but the ratios of corresponding sides are equal, that is

`(JK)/(GH)` =
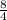`(8)/(4)` = 2 and
`(JL)/(GI)` =
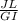`(10)/(5)` = 2

If the ratios of 2 pairs of corresponding sides of 2 triangles are equal and the included angles are congruent , then the triangles are similar, so

Δ GHI and Δ JKL are similar by the SAS postulate

C

the ratios of corresponding sides are equal , then

`(KL)/(HI)` =
`(JL)/(GI)`

`(KL)/(7)` =
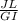
`(10)/(5)` = 2 ( multiply both sides by 7 to clear the fraction )

KL = 14