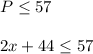Question

The length of the rectangle is X units more than its

width. The width of the rectangle is 11 units and the
length of the wire that is used to make this rectangle
is a maximum of 57 units. Represent this situation
using an inequality.

Answer 1

Answer:
`2x+44 \le 57\\\\`

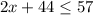
Step-by-step explanation:

W = width

W = 11

L = length

L = width+x

L = 11+x

P = perimeter of the rectangle

P = 2L+2W

P = 2*(11+x)+2*11

P = 22+2x+22

P = 2x+44

The perimeter is at max 57 units because it is the length of wire used. Think of it like fencing around a piece of land. Be sure not to mix up the length of the wire with the rectangle length; those are two different things.

Anyways, because the perimeter maxes out at 57, this means either P = 57 or P < 57.

This leads to:

`P \le 57\\\\2x+44 \le 57\\\\`