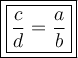Question

Which of the following is a true proportion of the figure based on the triangle proportionality theorem?

Answer 1

`\textsf{B)}\quad (c)/(d)=(a)/(b)`

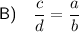
Explanation:

The Triangle Proportionality Theorem, also known as the Side Splitter Theorem, states that if a line is parallel to one side of a triangle and intersects the other two sides, then it divides those two sides proportionally.

In the given triangle, line segment TU is parallel to side QS, so TU divides sides RQ and RS proportionally.

Therefore, according to the triangle proportionality theorem:

`\sf \overline{RT} : \overline{TQ} = \overline{RU} : \overline{US}`

`c:d=a:b`

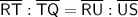
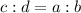
Therefore, the equation that is a true proportion of the figure based on the triangle proportionality theorem is:

`\large\boxed{\boxed{(c)/(d)=(a)/(b)}}`