Question

Dakota Shilah works for Arizona Bath Company as a repairman. He earns $12.00 for each fiberglass bathroom sink and $59 for each fiberglass tub enclosure he repairs. Last week he repaired a total of 23 items. Dakota’s pay for the week was $652. How many of each type of repair did he make?

Answer 1

GIVEN:

We are told that a repairman earns $12 for each bathroom sink he repairs and $59 for each tub he repairs.

Last week he repaired a total of 23 items and the total pay for the week was $652.

Required;

We are required to determine how many of each type of item did he repair.

Step-by-step solution;

We shall begin by assigning variables to the items and these will be;

Let fiberglass bathroom sink be x.

Let fiberglass tub be y.

if he repaired a total of 23 items, then we can set up the following equation;

`x+y=23---(1)`

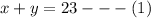
For each bathroom sink repaired he earns $12. That means if he repairs 2, then he would earn $12 times 2, and so on. This means if he repairs x number of fiberglass bathroom sink he would earn 12x.

The same applies to his fiberglass tub earnings. he would earn 59y if he repairs y number of tubs.

He makes a total of $652 for the week. That means for all his repairs, we can set up the following equation;

`12x+59y=652---(2)`

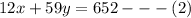
We can now solve the system of equations by using the substitution method;

`\begin{gathered} From\text{ }equation\text{ }(1),\text{ }make\text{ }x\text{ }the\text{ }subject\text{ }of\text{ }the\text{ }equation: \\ \\ x=23-y \\ \\ Substitute\text{ }the\text{ }value\text{ }of\text{ }x\text{ }into\text{ }equation\text{ }(2): \\ \\ 12(23-y)+59y=652 \end{gathered}`

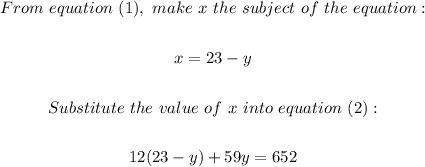
We can now simplify and we'll have;

`276-12y+59y=652`

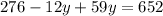
We can now collect like terms;

`59y-12y=652-276`

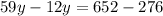
Note that the number 276 has crossed the equality sign and therefore has switched signs (from positive to negative).

`\begin{gathered} 47y=376 \\ \\ Divide\text{ }both\text{ }sides\text{ }by\text{ }47: \\ \\ y=8 \end{gathered}`

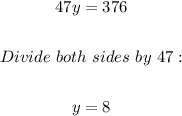
We can now substitute the value of y into equation (1);

`\begin{gathered} x+y=23 \\ \\ x+8=23 \\ \\ Subtract\text{ }8\text{ }from\text{ }both\text{ }sides: \\ \\ x=15 \end{gathered}`

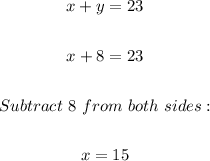
Therefore, we have

`\begin{gathered} x(bathroom\text{ }sink)=15 \\ \\ y(tub)=8 \end{gathered}`

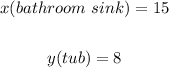
ANSWER:

The items he repaired during the week were;

15 fiberglass bathroom sink

8 fiberglass tub