n=8
Mean number of televesions per household= 4
Standard deviation= 1
Find the number of households have between 0 and 4 television
As a first step we are going to check the within numbers:
![\begin{gathered} \mu=\operatorname{mean} \\ \mu-x_1=4-0=4 \\ x_2-\mu=4-4=0 \end{gathered}]()
So, now, we can find the value of k:
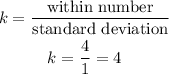
Now, using the chebychev's theorem:

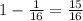
Then, the number of the house holds would be:
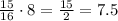
There are at least 7.5 households that have between 0 and 4 televisions