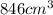Question

A 3-D printer is creating a shape that consists of what remains after a smaller cone has been removed from a larger cone, as shown below. Determine the volume, to the nearest cubic centimeter, of this object.

Answer 1

To answer this question we will use the following formula for the volume of a cone:

`\begin{gathered} V=(1)/(3)\pi r^2h, \\ where\text{ }r\text{ is }the\text{ cone radius and }h\text{ is its height.} \end{gathered}`

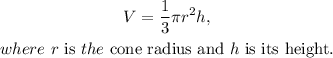
Notice that the volume of the given shape is the volume of the bigger cone minus the volume of the smaller cone.

The volume of the bigger cone is:

`\begin{gathered} V_G=(1)/(3)\pi *(10cm)^2*12cm \\ =400\pi cm^3. \end{gathered}`

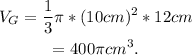
The volume of the smaller cone is:

`\begin{gathered} V_S=(1)/(3)\pi *(7cm)^2*8cm \\ =(392)/(3)\pi cm^3. \end{gathered}`

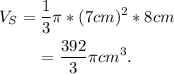
Therefore the volume of the given shape is:

`\begin{gathered} V=V_G-V_S=400\pi cm^3-(392)/(3)\pi cm^3 \\ =(808)/(3)\pi cm^3\approx846cm^3. \end{gathered}`

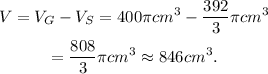
Answer:

`846cm^3`