Question

Question 10 Write the vector form of the velocity at time t=0sec.

Answer 1

Vertical component: 161 m/s

Horizontal component: 192 m/s

Step-by-step explanation:

Now the vertical component of velocity is found by

`\sin \theta=\frac{\text{opposite}}{\text{hypotenuse}}`

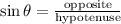
In our case

opposite = v_y

hypotenuse = v0 = 250 m/s

Therefore,

`\sin \theta=\frac{v_y_{}}{v_0}=\frac{v_y}{250_{}}`
`\sin \theta=(v_y)/(250)`

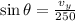
multiplying both sides by 250 gives

`250\sin \theta=v_y`

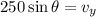
since Θ = 40, the above becomes

`250\sin (40^o)=v_y`

Evaluating the left-hand side gives

`v_y=160.697`

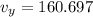
rounding to the nearest whole number

`\boxed{v_y=161.}`

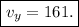
Hence, the vertical component of the velocity is 161 m/s.

Next, we find the horizontal component.

Now,

`\cos \theta=\frac{adjacent}{\text{hypotenuse}}`

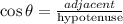
Now in our case

adajcent = v_x

hypotenuse = v0 = 250

therefore,

`\cos \theta=(v_x)/(v_0)=(v_x)/(250)`
`\Rightarrow\cos \theta=(v_x)/(250)`

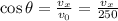
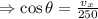
Multiplying both sides by 250 gives

`250\cos \theta=v_x`

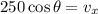
since Θ = 40, the above becomes

`250\cos (40^o)=v_x`

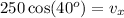
The left-hand side evaluates to give

`v_x=191.51111`

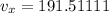
rounding to the nearest whole number gives

`\boxed{v_x=192.}`

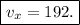
Hence, the horizontal component of the velocity is 192 m/s.