Question

I need help with question 7, I've included the prior answers from questions 3, 5, and 6 to help you. I've also included what the previous questions were so you have some context of the situation. Although, I think you only need the answers from part C ( which is the graph I've including) to answer question 7

Answer 1

The Solution to Question 7:

We are required to find the height of the blade when the Blade's angle is 570 degrees.

Recall:

`\begin{gathered} \angle570^o=570-360=\angle210^o \\ And \\ \angle210^o=210-180=\angle30^o \end{gathered}`

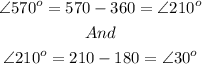
So, we shall find the height of the Blade when its angle is 210 degrees.

From the graph, we can see that the height of the Blade is from 150ft to 250ft and this gives a length of 100ft.

The given graph is only for 90 degrees.

So, 30 degrees out of 90 degrees is:

`\begin{gathered} (30)/(90)*100ft=33.33ft \\ \\ So,\text{ 150ft +33.33ft=183.33 feet} \end{gathered}`

Therefore, the correct answer is 183.33 feet