Recall that a rectangle has the following form
we must highlight form the picture that in a rectangle opposite sides are parallel. Recall that when talking about the equations of multiple lines, two lines are parallel if they have the same slope. Also, recall that the intercept-slope equation of a line is of the form y=mx+b where m is the slope and b is the y-intercept.
Based on this, what we should do is find the slope-intercept form of each equation, and then find two pair of lines that are parallel. To do so, we will first find the list of equations in slope-intercept form.
y+2x=8 -->y=-2x+8 (1)
2y=x-4 --> y=x/2 - 2 (2)
2y+1/2 x +1=0 -->y=-x/4-1/2 (3)
y+2x+2=0 -->y=-2x-2 (4)
2y+x=1 --> y=-x/2+1/2 (5)
y=x/2+2 (already in slope-intercept form) (6)
y=x-4 (already in slope-intercept form) (7)
y=4-x (already in slope-intercept form) (8)
y=2(x-1) = 2x-2 (9)
2y=4-x --> y=-x/2+2 (10)
From this, we can check that equations 1 and 4 have the same slope. Also, equations 2 and 6 have the same slope. The same happens with equations 5 and 10.
Also, note that in a rectangle, the sides form 90° angles. This means that the lines that lines that intercept should have different slopes, such that the product of their slopes are equal to -1. This implies that we should pick a pairs of lines such that:
1. One pair has positive slope.
2. One pair has a negative slope.
3. Their product should be -1.
Note that the only pair that has a positive slope is the pair 2 and 6, that have slope 1/2.
We can build the following equation to find the slope of the other pair

So by multiplying by 2 we get
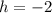
So the other pair should have slope -2. We see that the pair of equation 1 and 4. So the equation of our rectangle are
-->2y=x-4
-->y=x/2+2
-->y+2x=8
-->y+2x+2=0