Question

If x=1−sin a and y= 1+cos a, Express y in terms of x and a only ​

Answer 1

Explanation:

Given

`x=1-sin(a)\\y=1+cos(a)`

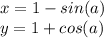
Solve for
`a` in the second equation.

`y=1+cos(a)`

`y-1=cos(a)`

`a=cos^(-1)( y-1)`

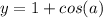
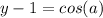
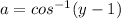
Insert our answer for
`a` into the first equation.

`x=1-sin(a)`

`x=1-sin(cos^(-1)( y-1))`

`cos^(-1)=arccos`

`x=1-sin(arccos( y-1))`

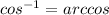
Lets simplify
`1-sin(arccos( y-1))`

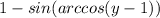
A piece of graph paper would be helpful in my opinion.

Here is how I would go about doing so

Draw a triangle in the plane with vertices
`(y-1,√(1^2-(y-1)^2)),(y-1,0)` and the origin.

`arccos(y-1)` is is the angle between the positive x-axis and the ray beginning at the origin and passing through
`(y-1,√(1^2-(y-1)^2))`. Therefore
`sin(arccos(y-1))` is
`√(1-(y-1)^2)`

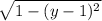
Now we have

`x-1-√(1-(y-1)^2)\\a=arccos(y-1)`

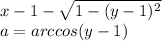
We can write
`1` as
`1^2`. Since both terms are now perfect squares, we can factor using the difference of squares formula.

`a^2-b^2=(a+b)(a-b)` where
`a=1` and
`b=y-1`

`x=1-√((1+y-1)(1-(y-1)))`

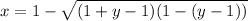
After simplifying we get

`x=-√(y(-y+2))+1`

`x=-√(y(-y+2))+1`

`a=arccos(y-1)`

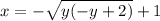
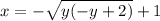
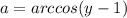
I think this is what your question was. If not let me know.