Question

Line q passes through points (6,8 )and( 3,4). Line r is perpendicular to q . What is the slope of line r

Answer 1

The slope of line r is -3/4

Explanation:

First, let's find the slope of line q. We can find the slope by finding the change in y over change in x.

`\displaystyle{m=(y_2-y_1)/(x_2-x_1)}`

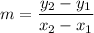
Therefore, substitute in:

`\displaystyle{m=(8-4)/(6-3)}\\\\\displaystyle{m=(4)/(3)}`

Therefore, the slope of line q is 4/3. Since we want to find the slope of line r and we know by the given that line r is perpendicular to line q. By the definition of perpendicular line is
`\displaystyle{m_1m_2=-1}`.

Let
`m_1` be slope of the line q which is 4/3. Therefore, substitute in and solve for
`m_2` (slope of line r)

`\displaystyle{(4)/(3)m_2=-1}\\\\\displaystyle{4m_2=-3}\\\\\displaystyle{m_2=-(3)/(4)}`

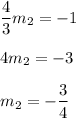
Therefore, the slope of line r is -3/4