Question

Solve the following problem.

1. If a is indirectly proportional to b, then a=k/b, where k is a constant or fixed number. If a=8 when b=6, find the value of k.

Using the value of k in number 1, find:
2. a if b=3
3. a if b=4
4. a if b=12
5. a if b=1.5
6. a if b=3.6
7. a if b=4.8
8. b if a=3
9. b if a=4
10. b if a=4.5
11. b if a= 4.8
12. b if a=3.6
13. b if a=6

Answer 1

see explanation

Explanation:

given the equation

a =
`(k)/(b)`

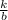
to find k use the given condition a = 8 when b = 6 , then

8 =
`(k)/(6)` ( multiply both sides by 6 to clear the fraction )

48 = k

a =
`(48)/(b)` ← equation of variation

2

if b = 3

a =
`(48)/(3)` = 16

3

if b = 4

a =
`(48)/(4)` = 12

4

if b = 12

a =
`(48)/(12)` = 4

5

if b = 1.5

a =
`(48)/(1.5)` = 32

6

if b = 3.6

a =
`(48)/(3.6)` = 13.3333.. = 13
`(1)/(3)`

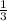
7

if b = 4.8

a =
`(48)/(4.8)` = 10

for the remaining questions, rearrange the equation with b as the subject

a =
`(48)/(b)` ( multiply both sides by b )

ab = 48 ( divide both sides by a )

b =
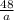
`(48)/(a)`

8

if a = 3

b =
`(48)/(3)` = 12

9

if a = 4

b =
`(48)/(4)` = 12

10

if a = 4.5

b =
`(48)/(4.5)` = 10.666... = 10
`(2)/(3)`

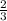
11

if a = 4.8

b =
`(48)/(4.8)` = 10

12

if a = 3.6

b =
`(48)/(3.6)` = 13.333... = 13
`(1)/(3)`

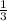
13

if a = 6

b =
`(48)/(6)` = 8