Answer:
![r=\frac{15\sqrt[3]{\pi ^2} }{\pi }](https://img.qammunity.org/2024/formulas/mathematics/college/jlvvxpu1mfkvm495fny02qczz14pb14q7l.png) meters
meters
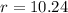 meters
meters
Explanation:
Here is the equation for the volume of a sphere
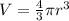
Lets solve for
 .
.
Multiply both sides of the equation by
 .
.
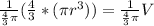
Simplify the left side.
Combine
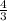 and
and
 .
.
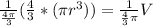
Multiply the numerator by the reciprocal of the denominator.

Cancel the common factor of
 by factoring it out of the first term.
by factoring it out of the first term.
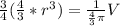
Combine
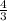 and
and
 .
.

Multiply the numerators on the left side of the equation. Then multiply the denominators.
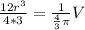
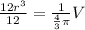
Cancel the common factor of 12.

Simplify the right side.
Combine
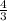 and
and
 .
.
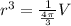
Multiply the numerator by the reciprocal of the denominator.
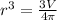
Take the cube root of both sides of the equation to eliminate the exponent on the left side.
![r=\sqrt[3]{(3V)/(4\pi ) }](https://img.qammunity.org/2024/formulas/mathematics/college/cuobrs5g1egbzg8b4ih3ra8nya1mz3b2vl.png)
Now we have an equation to find the radius.
Substituting our number for volume gives us
![r=\sqrt[3]{(3*4500)/(4\pi ) }](https://img.qammunity.org/2024/formulas/mathematics/college/dertseu9nvg9f1x7q8y5uvfuv3i4dr4e69.png)
Enter this into a calculator
![\sqrt[3]{(3*4500)/(4\pi ) }](https://img.qammunity.org/2024/formulas/mathematics/college/h44sz8qpx2ei3b1esolstveb9d3rhw0dkx.png)
You can leave the answer in simplest radical form or as a decimal.
![r=\frac{15\sqrt[3]{\pi ^2} }{\pi }](https://img.qammunity.org/2024/formulas/mathematics/college/jlvvxpu1mfkvm495fny02qczz14pb14q7l.png)
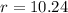
A rating/review would be much appreciated. Hope this helps!