Question

The populations P (in thousands) of a particular county from 1971 through 2014 can be modeled byP = 71.7e0.0345twhere t represents the year, with t = 1 corresponding to 1971.(a) Use the model to complete the table. (Round your answers to the nearest whole number.)YearPopulation1980101240 Correct: Your answer is correct.1990142949 Correct: Your answer is correct.2000201843 Correct: Your answer is correct.2010285000 Correct: Your answer is correct.(b) According to the model, when will the population of the county reach 350,000?2018 Incorrect: Your answer is incorrect.

Answer 1

ANSWERS

(a) Year - Population

• 1980 - 101,240

,

• 1990 - 142,949

,

• 2000 - 201,843

,

• 2010 - 285,000

(b) 2016

Step-by-step explanation

(a) The population (in thousands) each year is given by,

`P=71.7\cdot e^(0.0345t)`

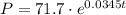
If t = 1 represents year 1971, then for each year we have to find the difference between the year and 1970.

For year 1980,

`P=71.7\cdot e^(0.0345(1980-1970))\approx101.240`

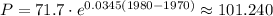
The population is 101,240.

For year 1990,

`P=71.7\cdot e^(0.0345(1990-1970))\approx142.949`

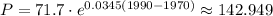
The population is 142,949.

For year 2000,

`P=71.7\cdot e^(0.0345(2000-1970))\approx201.843`

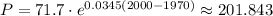
The population is 201,843.

For year 2010,

`P=71.7\cdot e^(0.0345(2010-1970))\approx285.000`

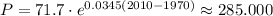
The population is 285,000.

(b) In this problem we're given the population 350,000 and we have to find in what year the county will reach that population. In other words, we have to find t and then add that to 1970 to find the year.

Let's solve for t,

`P=71.7\cdot e^(0.0345t)`

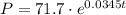
Divide both sides by 71.7,

`\begin{gathered} (P)/(71.7)=(71.7)/(71.7)\cdot e^(0.0345t) \\ (P)/(71.7)=e^(0.0345t) \end{gathered}`

Apply natural logarithm to both sides,

`\begin{gathered} \ln (P)/(71.7)=\ln e^(0.0345t) \\ \ln (P)/(71.7)=0.0345t \end{gathered}`

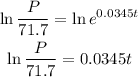
Divide both sides by 0.0345,

`\begin{gathered} (\ln (P)/(71.7))/(0.0345)=(0.0345t)/(0.0345) \\ (\ln(P)/(71.7))/(0.0345)=t \end{gathered}`

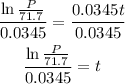
And finally replace P and solve. Remember that P is in thousands of years, so we have to replace it by 350,

`t=(\ln (350)/(71.7))/(0.0345)=45.955\approx46`

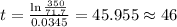
This is 46 years after 1970,

`1970+46=2016`

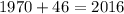
Let's see what's the population in 2016 to check the answer,

`P=71.7\cdot e^(0.0345(2016-1970))\approx350.546`

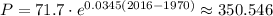
It is a bit more than 350,000. But let's see what's the population in 2015,

`P=71.7\cdot e^(0.0345(2015-1970))\approx338.658`

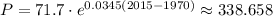
In 2015 population of the county won't reach 350,000. Thus, the county will have a population of 350,000 in 2016