Question

There were 23.7 million licensed drivers in California in 2009 and 22.76 in 2004. Find a formula for the number, N, of licensed drivers in the US as a function of t, the numbers of years since 2004, assuming growth isa) Linear N(t) = 0.188t + 22.76 million drivers b) Exponential N(t) =

Answer 1

`N(t)=22.76(1.0081)^t`

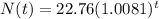
Step-by-step explanation:

The exponential function is of the form:

`N(t)=a(b)^t`

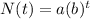
In 2004, (i.e. t=0), the number of licensed drivers = 22.76 million

`\begin{gathered} N(t)=22.76,t=0 \\ 22.76=a(b)^0 \\ \implies a=22.76 \end{gathered}`

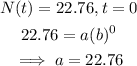
In 2009, the number of licensed drivers = 23.7 million

`\begin{gathered} a=22.76,N(t)=23.7,t=2009-2004=5 \\ N(t)=a(b^t)\implies23.7=22.76(b)^5 \end{gathered}`

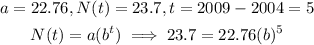
We solve for the value of b:

`\begin{gathered} 23.7=22.76(b)^5 \\ b^5=(23.7)/(22.76) \\ b=\sqrt[5]{(23.7)/(22.76)} \\ b=1.0081 \end{gathered}`

Therefore, an exponential formula for the number, N, of licensed drivers in the US as a function of t, the numbers of years since 2004 is:

`N(t)=22.76(1.0081)^t`

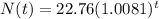
Note: N(t) is in millions