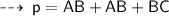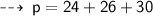Question

For triangle ABC use the Triangle Proportionality Theorem to solve for x

1. what is the value of x?

2. What is the perimeter of triangle ABC?

show ALL work-- PLEASE HELP!

Answer 1

`{ \qquad\qquad\huge\underline{{\sf Answer}}}`

Here's the solution ~

The two triangles in the shown figure are similar, therefore conclusion can be made that :

Ratio of its it's corresponding sides is equal.

`\qquad \sf  \dashrightarrow \: (2x - 4 + 6)/(6) = (24)/(4)`

`\qquad \sf  \dashrightarrow \: (2x + 2)/(6) = 6`

`\qquad \sf  \dashrightarrow \: 2x + 2 = 6 * 6`

`\qquad \sf  \dashrightarrow \: 2x + 2 = 36`

`\qquad \sf  \dashrightarrow \: 2x = 36 - 2`

`\qquad \sf  \dashrightarrow \: 2x = 34`

`\qquad \sf  \dashrightarrow \: x = 17`

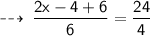
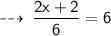
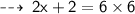
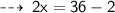
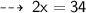
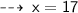
Therefore, The value of x is " 17 "

Now, the measure of side BC is :

`\qquad \sf  \dashrightarrow \: 2x - 4`

`\qquad \sf  \dashrightarrow \:2 (17) - 4`

`\qquad \sf  \dashrightarrow \: 34 - 4`

`\qquad \sf  \dashrightarrow \: 30 \: \: units`

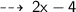
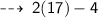
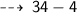
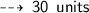
So, its perimeter will be :

`\qquad \sf  \dashrightarrow \: p = AB + AB + BC`

`\qquad \sf  \dashrightarrow \: p = 24 + 26 + 30`

`\qquad \sf  \dashrightarrow \: p = 80 \: \: units`

Answer 2

• 1) x = 17,
• 2) P = 86 units.

------------------------------------

Part 1

According to Triangle Proportionality Theorem we have the following equal proportions:

• (24 - 4)/4 = (2x - 4)/6
• 20/4 = (x - 2)/3
• 5 = (x - 2)/3
• x - 2 = 5*3
• x - 2 = 15
• x = 17

Part 2

The missing side is:

• BC = 6 + 5*6 = 6 + 30 = 36 units

The perimeter is:

• P = 24 + 36 + 26 = 86 units