Question

A ball is launched from a 48.314-meter tall platform. The equation

=
for the ball's height h at time t seconds after launch is h (t) =
-4.9t² +2.45t + 48.314, where his in meters. When does the
object strike the ground?

Answer 1

3.4 seconds

Explanation:

Given function:

`h(t)=-4.9t^2+2.45t+48.314`

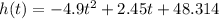
where

• h = height of the ball (in meters)
• t = time (in seconds)

The ball will strike the ground when its height is zero.

Therefore, to calculate when the ball strikes the ground, substitute h(t) = 0 and solve for t using the quadratic formula.

`\boxed{\begin{minipage}{3.6 cm}\underline{Quadratic Formula}\\\\$x=(-b \pm √(b^2-4ac))/(2a)$\\\\when $ax^2+bx+c=0$ \\\end{minipage}}`

Therefore:

• a = -4.9
• b = 2.45
• c = 48.314

Substitute these values into the quadratic formula:

`\implies t=(-2.45 \pm √((2.45)^2-4(-4.9)(48.314)))/(2(-4.9))`

`\implies t=(-2.45 \pm √(6.0025+946.9544))/(-9.8)`

`\implies t=(-2.45 \pm √(952.9569))/(-9.8)`

`\implies t=(-2.45 \pm 30.87)/(-9.8)`

`\implies t=(-2.45 + 30.87)/(-9.8)=-2.9`

`\implies t=(-2.45 -30.87)/(-9.8)=3.4`

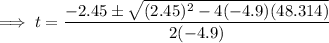
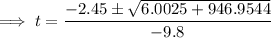
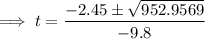
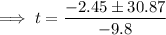
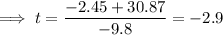
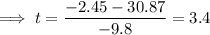
As time cannot be negative, t = 3.4 s only.

Therefore, the ball strikes the ground 3.4 seconds after it is launched.