Question

Batman shoots a grappling hook

34.6 m/s at an 80.2° angle. What is the magnitude only (no direction) of the velocity of the hook 1.09 s later?

(Unit = m/s)

Answer 1

24.132 m/s

Step-by-step explanation:

Note

`U` = Initial Velocity

`U_x` = Initial Horizontal Velocity

`U_y` = Initial Vertical Velocity

`V` = Final Velocity

`V_x` = Final Horizontal Velocity

`V_y` = Final Vertical Velocity

`B` = launch angle

`g` = gravity

`t` = time

`U_x=U*cos(B)`

`U_y=U*sin(B)`

The horizontal component of the velocity is constant throughout the flight. So
`U_x=V_x` It can be defined as

`V_x=U*cos(B)`

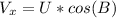
We can use the kinematics equation

`V=U+at`

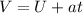
Gravity is acting downwards; gravity would be negative

`V_y=U_y-gt`

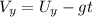
The magnitude of the velocity can be defined as

`V=√(V_x^2+V_y^2)`

Inserting some of the other equations gives us an equation at a given time (t).

`V=√((U*cos(B))^2+(U*sin(B)-gt)^2)`

`V=\sqrt{(UcosB)^2+(UsinB)^2+(gt)^2-2gtU*sinB`

`V=√(U^2+g^2*t^2-2*t*g*U*sinB)`

`V(t)=√(U^2+g^2t^2-2tgUsinB)`

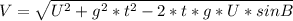
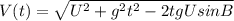
We are given

`U=34.6`

`B=80.2`

`t=1.09`

`g=9.81`

`V(1.09)=√(34.6^2+9.81^2*1.09^2-2*1.09*9.81*34.6*sin80.2)`

`V(1.09)=√(34.6^2+114.338-2*1.09*9.81*34.6*sin80.2)`

`V(1.09)=√(34.6^2+114.338-739.94868*sin80.2)`

`V(1.09)=√(34.6^2+114.338-729.151)`

`V(1.09)=√(1197.16+114.338-729.151)`

`V(1.09)=√(582.347)`

`V(1.09)=24.132`

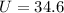
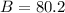
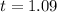
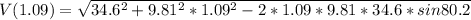
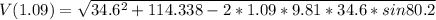
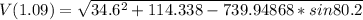
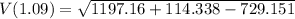
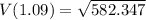
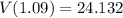
A rating/review would be much appreciated. Hope this helps!

Let me know if you have any questions about my work