Question

Write an equation of a line that passes through the point (3, 2) and is parallel to the line y = 3x - 4.

y = 3x + 7
y = 3x - 7
y= 1/3x+2
y=1/3x-2

Answer 1

`y=3x-7`

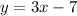
Explanation:

Parallel Lines:

Parallel lines, by definition, never intersect. They have the same slope but different y-intercepts (otherwise they would be the same line) on a graph.

Slope-Intercept Form:

Slope-Intercept form is expressed as:
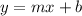`y=mx+b`, where

• 
  `m = \text{slope}`
• 
  `b = \text{y-intercept}`

This form is super useful for linear equations as it gives us the two key features of a linear equation. It's how each of the options are formatted, so we know we'll have to use this form.

Generally Finding a Parallel Line:

The line is parallel to
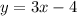`y=3x-4`, meaning it has a slope of 3, but also a y-intercept other than -4 (otherwise they would be the same equation).

So we can generally form an equation:
`y=3x+b\text{, }b\\e-4`, so we can plug any value for "b" here (except -4) and have a parallel line

Finding a line passing through a point:

Since we not only want to find a parallel line, but also one that passes through a specific point, we can use our general parallel equation:
`y=3x+b\text{, }b\\e-4`, and plug in known values. We of course already have the slope plugged in, but now we have a (x, y) coordinate, which we can plug in for x and y in the equation.

Original Equation:

`y=3x+b`

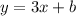
Point given: (3, 2), substitute in x=3 and y=2:

`2=3(3)+b`

Simplify:

`2=9+b`

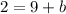
Subtract 9 from both sides:

`-7=b`

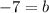
Now we can take this value. and plug it back into the general equation:

`y=3x+(-7)\implies y=3x-7`

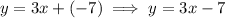
Now we have our answer!