Answer:
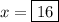
Explanation:
Since $x$ is a positive multiple of 8, it must be at least 8. Since $x^2>100$ and $x$ is at least 8, the only solution is $x=16$.
To verify this, note that $x=8$ does not satisfy the inequality $x^2>100$, but $x=16$ does, so $x=16$ is the only solution that works.
Therefore, $x=\boxed{16}$.