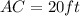Question

A sprinkler system is set up to water the sector shown in the accompanying diagram, with angle ABC measuring 1 radian and radius AB = 20 feet. What is the length of arc AC, in feet?

Answer 1

The length of the arc AC is;

`AC=20ft`

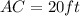
Step-by-step explanation:

Given the radius AB as 20ft.

`AB=20\text{ ft}`

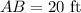
And angle ABC measures 1 radian.

Using the Method 1;

Length of Arc AC is;

`AC=\omega r`

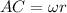
Substituting the angle in radian and the radius;

`\begin{gathered} AC=1*20\text{ ft} \\ AC=20\text{ ft} \end{gathered}`

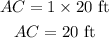
The length of Arc AC is 20 ft

Method 2;

We will firstly convert the angle from radian to degree.

As shown below;

`\begin{gathered} \theta=1\text{ rad}*(180)/(\pi) \\ \theta=57.3^0 \end{gathered}`

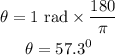
Then we will apply the formula for calculating the length of an arc;

`C=(\theta)/(360)*2\pi r`

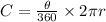
Substituting the value of the angle and the radius.

`\begin{gathered} C=(57.3)/(360)*2\pi*20ft \\ C=(57.3)/(360)*40\pi ft \\ C=20ft \end{gathered}`

Therefore, the length of the arc AC is;

`AC=20ft`