Answer:
Increasing:
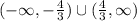
Decreasing:
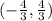
Explanation:
A continuous function increases where
 and decreases where
and decreases where
 , so let's find our critical points:
, so let's find our critical points:
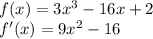
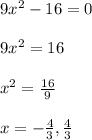
We'll use
 as test points to see how the derivative's behavior is around the critical points:
as test points to see how the derivative's behavior is around the critical points:
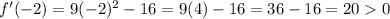
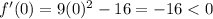
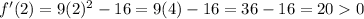
Hence, we can see that f(x) increases on the interval
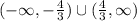 and decreases on the interval
and decreases on the interval
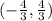 .
.