Given m(x) and n(x), the rational function m(x)/n(x) is
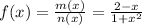
a) The zeroes of the function are the values of x such that f(x)=0; then,
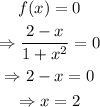
The zero of the function is at x=2.
b) Notice that the limits when x->+/- infinite are
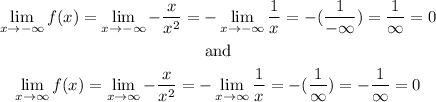
This implies that there is an asymptote at y=0; however, notice that
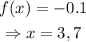
Thus, the graph of f(x) crosses y=0; thus, there are no asymptotes even if the behavior of the function tends to zero.
c) The function's domain consists of every value of x such that the denominator of f(x) is different than zero. Notice that 1+x^2>=1 since x^2>=0; thus

d) n(x) and m(x) are polynomial function; thus both functions are continuous. Then,
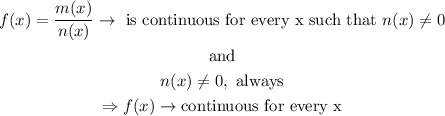
Therefore, the rational function is indeed continuous for any value of x.
e) As we stated before, f(x) is defined for every value of x such that n(x) is different than zero, and n(x)>1 for every x. Thus, there are no values of x such that m(x)/n(x) is undefined.
f) As for the end behavior of the function, we found that the limits when x approaches +/- infinite are equal to zero. Therefore, the end behavior of the function is not positive nor negative since 0=-0