Question

50 POINTS

Which equation represents a tangent function with a domain of all Real numbers such that x is not equal to pi over 4 plus pi over 2 times n comma where n is an integer?


f (x) = tan(2x – π)

g(x) = tan(x – π)

h of x equals tangent of the quantity x minus pi over 2 end quantity

j of x equals tangent of the quantity x over 2 minus pi end quantity

Answer 1

A) f(x) = tan(2x - π)

Explanation:

`\boxed{\begin{minipage}{8.3cm}\underline{Standard form of a tangent function}\\\\$f(x)=A \tan(B(x+C))+D$\\\\where:\\\\\phantom{ww}$\bullet$ $A=$ vertical stretch\\ \\\phantom{ww}$\bullet$ $(\pi)/(|B|)=$ period\\\\\phantom{ww}$\bullet$ $C=$ horizontal shift (positive is to the left)\\\\\phantom{ww}$\bullet$ $D=$ vertical shift\\\end{minipage}}`

The parent tangent function is:

`f(x)=\tan(x)`

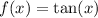
The period of the parent tangent function is π.

A tangent function is discontinuous when cos(x) = 0, so it has vertical asymptotes whenever cos(x) = 0.

Therefore, the parent tangent function has vertical asymptotes at:

`x=(\pi)/(2)+\pi n`

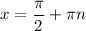
and so its domain is:

`\left\{ x \in \mathbb{R} \;| \;x \\eq (\pi)/(2)+\pi n\right\}`

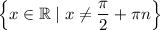
If the domain of the given tangent function is:

`\left\{ x \in \mathbb{R} \;| \;x \\eq (\pi)/(4)+(\pi)/(2)n\right\}`

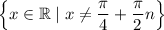
then its vertical asymptotes are when:

`x =(\pi)/(4)+(\pi)/(2)n`

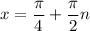
Therefore, its period is π/2.

`\implies (\pi)/(|B|)=(\pi)/(2)`

`\implies B=2`

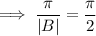
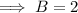
And it has been horizontally shifted by π/2:

`\implies f(x)=\tan\left(2\left(x-(\pi)/(2)\right)\right)`

`\implies f(x)=\tan\left(2x-\pi\right)`

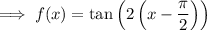
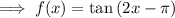
Function g(x)

`g(x)=\tan(x- \pi)`

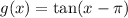
• Period = π
• Horizontal shift = π
• Vertical asymptotes = π/2 + πn

Function h(x)

`h(x)=\tan \left(x-(\pi)/(2)\right)`

• Period = π
• Horizontal shift = π/2
• Vertical asymptotes = π + πn

Function j(x)

`j(x)=\tan \left((x)/(2)- \pi \right)`

• Period = 2π
• Horizontal shift = 2π
• Vertical asymptotes = π + 2πn