Question

Prove that the product of the slopes of lines AC and BC is -1. Select each answer from the drop down menu.

Answer 1

Ok so the first drop menu has the reason why the sum of angles FCG, GCE and ECD is equal to the angle FCD. As you can see the apertures of all these three angles combined are equal to that of FCD so the answer to the first menu is angle addition.

The second drop-down menu gives us the reason behind the following simplification:

`\begin{gathered} 180=\angle FCG+90+\angle ECD \\ 90-\angle FCG=\angle ECD \end{gathered}`

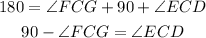
If we take the first equation and we use the substracting property of the equality by substracting the term 90+FCG from both sides we get:

`\begin{gathered} 180-(\angle FCG+90)=\angle FCG+90+\angle ECD-(\angle FCG+90) \\ 180-\angle FCG-90=\angle FCG+90+\angle ECD-\angle FCG-90 \\ 90-\angle FCG=\angle ECD \end{gathered}`

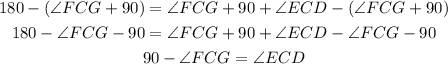
So the reason behind the simplification and answer to the second menu is the substraction property of equality.

The third drop-down menu gives us the reason behind the following equality:

`(GF)/(CD)=(FC)/(DE)`

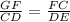
We know that triangles GFC and CDE are similar. Then the following pairs of sides are corresponding:

`\begin{gathered} GF\leftrightarrow DE \\ FC\leftrightarrow CD \end{gathered}`

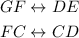
The products between corresponding angles are all the same because they are proportional. This means that:

`GF\cdot DE=FC\cdot CD`

If we divide both sides by DE*CD we get:

`(GF)/(CD)=(FC)/(DE)`

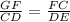
Which is the equality we had at the beginning. This means that the answer to the third menu is corresponding sides of similar triangles are proportional.

In the fourth menu we have the reason behind this operation:

`(GF)/(FC)=(CD)/(DE)\rightarrow(GF)/(FC)\cdot(-DE)/(CD)=(CD)/(DE)\cdot(-DE)/(CD)`

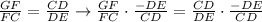
As you can see the operation consist on multiplying the same term (-DE/CD) at both sides of an equality. The multiplication property of the equality states that if we have:

`a=b`

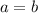
Then we also have:

`a\cdot c=b\cdot c`

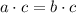
This exactly what was used in the last operation. This means that the answer to the fourth menu is the multiplication property of equality.