Question

GEOMETRY FIND LENGTH OF THIRD SIDE!!

Answer 1

Answer: 4

Explanation:

With the pythagorean theorem, a²+b²=c².

C² is always the hypotenuse, which in this case is
`2\sqrt 5\\`. The length of the base, a², is 2, ad we don't know b so we'll substitute it as "x".
So...
(2)²+(x)²=
`(2√(5) )^2`.

Simplify to get 4+(x)²=(
`2√(5) \\`)².

Now, to write as a single radical, we need to square the two ("undoing" the square root). So, we get (
`√(4) *\sqrt{5\\` )², which is (
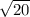`√(20)`)². Since we're squaring a square root, the square root almost "cancels out", leaving just the 20.

Now going back to our pythagorean theorem equation,

4+(x)²=20. Now we can subtract 4, getting (x)²=16. Hence, x= ± 4, and since a side can't be egative, it's just 4.

VERIFICATION: (4)²+(2)²=20, =16+4=20 ✓

Answer 2

It's 4

Explanation:

Trust the math