Question

Please help me answer this question.

Answer 1

B

Explanation:

Answer 2

A) Functions A and B have the same y-intercept.

Explanation:

`\boxed{\begin{minipage}{6.3 cm}\underline{Slope-intercept form of a linear equation}\\\\$y=mx+b$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $b$ is the $y$-intercept.\\\end{minipage}}`

Function A is a linear equation in slope-intercept form.

Therefore:

• Slope = -3
• y-intercept = 2

x-intercept

The x-intercept is when y = 0.

`\begin{aligned}\textsf{$x$-intercept of Function A}: \quad -3x+2&=0\\-3x&=-2\\x&=(2)/(3)\end{aligned}`

Reading from the table, the x-intercept of Function B is x = 4.

Therefore, the two functions do not have the same x-intercept.

y-intercept

The y-intercept is when x = 0.

We have already determined that the y-intercept of Function A is y = 2.

Reading from the table, the y-intercept of Function B is also y = 2.

Therefore, both functions have the same y-intercept.

Linear function

A linear function has one independent variable and one dependent variable. The highest exponent of both variables is one.

Therefore, Function A is a linear function.

In a linear relationship, as one variable increases/decreases the other variable changes at the same rate.

For Function B, every time x increases by 2 units, y decreases by 1 unit.

Therefore, Function B is also a linear function.

Slope

We have already determined that the slope of Function A is -3.

`\boxed{\sf Slope=(change\:in\:y)/(change\:in\:x)}`

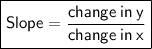
For Function B, every time x increases by 2 units, y decreases by 1 unit for Function B. Therefore, the slope of Function B is -¹/₂.

As 3 > ¹/₂, the slope of Function A is steeper than the slope of Function B.