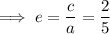Question

For questions 9-12, use the ellipse having foci located at (3,1) and (7,1), and a major axis length of 10.

9. what are the coordinates of the vertices.
10. What is the length of the minor axis.
11. find the eccentricity of the ellipse.
12. draw a sketch of the ellipse. PLEASE HELP AND SHOW WORK!

Answer 1

`\textsf{9.} \quad \textsf{Vertices}:\;\;(0, 1) \;\; \textsf{and} \;\; (10, 1)`

`\textsf{10.} \quad \textsf{Minor axis}:\;\;2√(21)`

`\textsf{11.} \quad \textsf{Eccentricity}:\;\;(2)/(5)`

`\textsf{12.} \quad \sf See\;attachment`

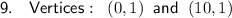
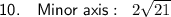
Explanation:

`\boxed{\begin{minipage}{9.2 cm}\underline{General equation of an ellipse}\\\\$((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1$\\\\where:\\\phantom{ww}$\bullet$ $(h,k)$ is the center\\ \phantom{ww}$\bullet$ $(h\pm a,k)$ or $(h,k\pm b)$ are the vertices\\ \phantom{ww}$\bullet$ $(h\pm c,k)$ or $(h,k\pm c)$ are the foci where $c^2=a^2-b^2$\\\end{minipage}}`

Given:

• Foci: (3, 1) and (7, 1)
• Major axis: 10

The center of an ellipse is the midpoint of the foci.

Therefore, the center (h, k) of the ellipse is (5, 1), so:

• h = 5
• k = 1

The foci are on the major axis of an ellipse.

Given that the y-values of the given foci are the same, the ellipse is horizontal.

The foci of a horizontal ellipse are (h±c, k)

`\implies 5-c=3 \implies c=2`

`\implies 5+c=7 \implies c=2`

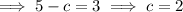
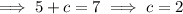
The major axis of a horizontal ellipse is 2a.

If the major axis is 10, then a = 5.

The vertices of a horizontal ellipse are (h±a, k).

Therefore the coordinates of the vertices are:

• (5-5, 1) = (0, 1)
• (5+5, 1) = (10, 1)

The minor axis of a horizontal ellipse is 2b.

As c² = a² - b² then b = √(a² - c²).

`\implies b=√(5^2-2^2)=√(21)`

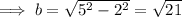
Therefore, the minor axis is 2√(21).

The eccentricity of the ellipse is:

`\implies e=(c)/(a)=(2)/(5)`