Question

The volume of gas a balloon can hold varies directly as the cube of its radius. Imagine a balloon with a radius of 4 inches can hold 192 cubic inches of gas. How many cubic inches of gas must be released to reduce the radius down to 3 inches?

Answer 1

To reduce the radius down to 3 inches, we must release 111 cubic inches of gas.

Step-by-step explanation:

To solve this problem, we need to use the direct variation formula, which states that the volume of the balloon varies directly as the cube of its radius. Let's denote the initial volume of the balloon as V1, the initial radius as r1, the new volume as V2, and the new radius as r2.

We are given that when the radius is 4 inches, the volume is 192 cubic inches. Using this information, we can set up the proportional equation:

`V1/r1^3 = V2/r2^3`

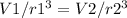
Substituting the given values, we have:

`192/4^3 = V2/3^3`

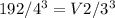
Simplifying the equation, we get:

192/64 = V2/27

Cross-multiplying, we find that:

V2 = (192/64) * 27

= 81 cubic inches

Therefore, to reduce the radius down to 3 inches, we must release 111 cubic inches of gas.

Answer 2

Answer:111

Step-by-step explanation: