Answer:
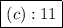
Explanation:
We can think of this problem as placing $7$ dividers (representing the boys) in $20$ slots (representing the people). Thus, the number of ways to arrange the boys and girls is the number of ways to place the dividers, which is $\binom{20}{7}$.
To find the average value of $S$, we need to find the total number of arrangements where $S = k$ for each possible value of $k$, then divide by the total number of arrangements.
Let's first consider the case where $k=0$. There is only $1$ way to arrange the boys and girls such that there are no boys and girls standing next to each other: BBBBBBBBBBBBBBBBBBBBB.
Next, let's consider the case where $k=1$. There are $\binom{7}{1}\binom{13}{6}$ ways to arrange the boys and girls such that there is exactly $1$ pair of boys and girls standing next to each other. To see this, consider that there are $\binom{7}{1}$ ways to choose the position of the divider that separates a boy and a girl, and $\binom{13}{6}$ ways to arrange the remaining dividers and slots.
We can continue this process to find the total number of arrangements for each possible value of $k$. When we add up all of these arrangements and divide by the total number of arrangements, we get the average value of $S$.
More specifically, the average value of $S$ is equal to
[\frac{1\cdot1+\binom{7}{1}\binom{13}{6}\cdot1+\binom{7}{2}\binom{13}{5}\cdot2+\binom{7}{3}\binom{13}{4}\cdot3+\binom{7}{4}\binom{13}{3}\cdot4+\binom{7}{5}\binom{13}{2}\cdot5+\binom{7}{6}\binom{13}{1}\cdot6+\binom{7}{7}\binom{13}{0}\cdot7}{\binom{20}{7}}.]
Simplifying this expression gives us $\boxed{(c) : 11}$.