Question

Suppose that the function f is defined, for all real numbers, as follows.


`f(x)\left \{ {{x-3 IF x \leq -2} \atop {4x+5IFx\ \textgreater \ -2}} \right.`
Graph the function f. Then determine whether or not the function is continuous.

Answer 1

See attached graph

Graph is not continuous

Explanation:

The function is not continuous as you can see from the break in the graph

It is discontinuous at x = -2

Answer 2

See attachment for graph.

The function is not continuous.

Explanation:

Piecewise functions have multiple pieces of curves/lines where each piece corresponds to its definition over an interval.

Given piecewise function:

`f(x)=\begin{cases} x-3 \;\;\;\;\: \text{if}\;\;\;x \leq -2\\4x+5 \;\;\; \text{if}\;\; \;x > -2 \end{cases}`

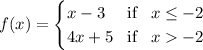
Therefore, the function has two definitions:

• f(x) = x - 3 when x is less than or equal to -2.

• f(x) = 4x + 5 when x is greater than -2.

When graphing piecewise functions:

• Use an open circle where the value of x is not included in the interval.
• Use a closed circle where the value of x is included in the interval.
• Use an arrow to show that the function continues indefinitely.

First piece of the function

Substitute x = -2 into the first function:

`\implies f(-2)=-2-3=-5`

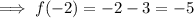
As the interval for the first equation is x ≤ -2, it includes the value of x = -2. Therefore, place a closed circle at point (-2, -5).

To help graph the line, find another point on the line by inputting another value of x that is less than -2 into the same function:

`\implies f(-5)=-5-3=-8`

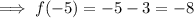
Plot point (-5, -8) and draw a straight line from the closed circle at (-2, -5) through (-5, -8). Add an arrow at the other endpoint to show it continues indefinitely as x → -∞.

Second piece of the function

Substitute x = -2 into the second function:

`\implies f(-2)=4(-2)+5=-3`

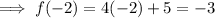
As the interval for the second equation is x > -2, it does not include the value of x = -2. Therefore, place an open circle at point (-2, -3).

To help graph the line, find another point on the line by inputting another value of x that is more than -2 into the same function:

`\implies f(1)=4(1)+5=9`

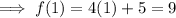
Plot point (1, 9) and draw a straight line from the open circle at (-2, -3) through (1, 9). Add an arrow at the other endpoint to show it continues indefinitely as x → ∞.

See attachment for the graph.

`\boxed{\begin{minipage}{8cm}\underline{Determining if a function is continuous at $x=a$}\\\\Condition 1: $f(a)$ exists\\\\Condition 2: $\displaystyle \lim_(x \to a)f(x)$ exists at $x=a$\\\\Condition 3: $\displaystyle \lim_(x \to a)f(x)=f(a)$\\\end{minipage}}`

If all three conditions are satisfied, the function is continuous at x = a.

If any one of the conditions is not satisfied, the function is not continuous at x = a.

To determine whether or not the given piecewise function is continuous, find if the function is continuous at x = -2.

Condition 1

Does f(-2) exist? Yes → f(-2) = -5

Condition 2

`\textsf{Does}\;\;\displaystyle \lim_(x \to -2) f(x)\;\; \sf exist\;at\;\;x=-2?`

To the left of x =- 2, f(x) = x - 3

To the right of x = -2 , f(x) = 4x + 5

Evaluate the left and right limits as x approaches -2:

`\displaystyle \lim_(x \to -2^-)f(x)=\lim_(x \to -2^-) -2-3=-5`

`\displaystyle \lim_(x \to -2^+)f(x)=\lim_(x \to -2^+) 4(-2)+5=-3`

`\textsf{As}\;\;\displaystyle \lim_(x \to -2^-) f(x) \\eq \lim_(x \to -2^+) f(x), \;\; \lim_(x \to -2) f(x)\;\; \textsf{does not exist}.`

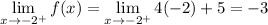
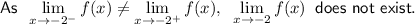
As condition 2 fails, there is no need to proceed to condition 3.

Therefore, the function is not continuous.