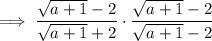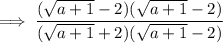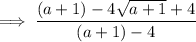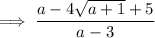Question

Rationalize the denominator and simplify. √(a+1)-2 / √(a+1)+2​

Answer 1

`(a-4√(a+1)+5)/(a-3)`

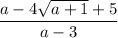
Explanation:

Given rational expression:

`(√(a+1)-2)/(√(a+1)+2)`

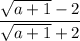
To rationalize the denominator, multiply the numerator and denominator by the conjugate of the denominator.

The conjugate of a binomial is where we change the sign between the two terms of the binomial. So the conjugate of √(a+1)+2​ is √(a+1)-2​.

Therefore:

`\implies (√(a+1)-2)/(√(a+1)+2) \cdot (√(a+1)-2)/(√(a+1)-2)`

`\implies ((√(a+1)-2)(√(a+1)-2))/((√(a+1)+2)(√(a+1)-2))`

`\implies ((a+1)-4√(a+1)+4)/((a+1)-4)`

`\implies (a-4√(a+1)+5)/(a-3)`