Question

A line is perpendicular to y = -x-2

and intersects the point (-5, 10).
What is the equation of this
perpendicular line?
y = x + [?]
Hint: Use the Point-Slope Form: y - y₁ = m(x - X1)
Then write the equation in slope-intercept form.
H

Answer 1

Point-Slope form: y-10=x(x+5)
Slope-intercept form: Y=x + 15

Answer 2

To find the equation of a line that is perpendicular to the line y = -x - 2 and intersects the point (-5, 10), we can use the Point-Slope Form of a line: y - y₁ = m(x - X1)

The Point-Slope Form allows us to find the equation of a line when we know the slope of the line (m) and the coordinates of a point on the line (X1, Y1).

In this case, we know that the slope of the line y = -x - 2 is -1, because the coefficient of x is -1. We also know that the line intersects the point (-5, 10), so we can substitute those values into the Point-Slope Form:

`y - 10 = -1(x - (-5))\\`

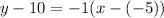
Next, we can simplify this equation by distributing the -1:

`y - 10 = -1x + 5`

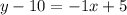
Finally, we can write the equation in slope-intercept form by adding 10 to both sides and simplifying:

`y = -1x + 15`

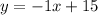
So, the equation of the line that is perpendicular to y = -x - 2 and intersects the point (-5, 10) is y = 1x+15.

I hope this helps! If you have any questions about this problem or if you need further clarification, just let me know.