Question

The dollar value vt of a certain car model that is t years old is given by the following exponential function.

v(t)= 25,900(0.90)^2
Find the initial value of the car and the value after 11 years.
Round your answers to the nearest dollar as necessary.

Initial Value:
Value after 11 years:

Answer 1

$25,900 initially

$8,128 after 11 years

Explanation:

One thing to note, is I'm assuming you meant:
`v(t)=25,900(0.90)^t` and not
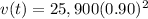`v(t)=25,900(0.90)^2`, otherwise that would just be a constant function and not an exponential function.

Exponential Function Key Features:

There are a couple key features of exponential functions we can derive from simply analyzing the equation.

For now I will be using the form:
`y=a(b)^x\text{ where b} > 0, \text{b}\\e 1`

y-intercept:

The y-intercept, is just the "a" value, which is because the y-intercept is simply when x=0, and if we raise a number to the power of zero, we get one (excluding zero as a base), so we get the form:
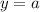`y=a`, so "a" is our y-intercept.

Rate of Change:

there's actually two type of exponential functions: exponential growth and exponential decay.

Exponential Decay:

Exponential decay, as the name implies, is when a function is decaying or decreasing. This occurs when
`0 < b < 1`.

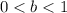The decay rate can be represented as "r" in decimal form, where:
`b=1-r`.

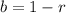The reason for this is because "1" can be thought of as 100% and "r" is r%, so you're taking away r% or decaying the value by r%, also known as a decay rate.

Exponential Growth:

Exponential growth as the name implies, is when a function is growing or increasing. This occurs when b > 1

The growth rate can be represented as "r" in decimal form where:
`b=1+r`

The reason for this is similar to decay rate except instead of taking away r% or decaying, it's "giving r%" or growing.

Solving the Question:

The question doesn't actually require finding exponential growth or decay, but it's still an important key feature.

In this case, we really just need to find the y-intercept and plug in t=11.

The y-intercept in many graphs, not just exponential graphs, represents some sort of initial value, which in this case, is the initial value of the car. As stated above, this y-intercept is just the value in front, which is 25,900.

As for the value after 11 years, we simply need to plug in t=11 to get the following:
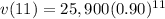`v(11)=25,900(0.90)^(11)`, from here we can use a calculator to simplify this:
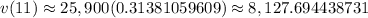`v(11)\approx25,900(0.31381059609)\approx 8,127.694438731`, which rounds to 8,128