Question

A model rocket is launched. The height, in feet, of the rocket h(t) at t (t≥ 0) seconds after

determined by the equation h(t):
-1/2t^2+ 15t. The maximum height of the rocket is 112.5 feet. For how many seconds will the rocket be at a height of more than 100 feet?

Answer 1

Answer: 36.902 Seconds

Explanation:

(1) --> To find the time that the rocket is at a height of more than 100 feet, you need to find the time when the height of the rocket is equal to 100 feet.

(2) --> do this by setting your equation equal to 100

`(-(1)/(2) )t^2 + 15t = 100`

`(-(1)/(2)) t^2 + 15t - 100 = 0`

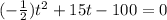
(3) --> From here, use the quadratic formula to solve for t

Quadratic formula:

`t = - (-b+-√(b^2 - 4ac) )/(2a)` (solving the b+ first)

`t = \frac{(-15 + \sqrt{225 - 4(-(1)/(2)) (-100)}}{-1}`

`= ((-15 + √(475)))/(-1)`

`= ((-15 + 21.902))/(-1)`

`= (6.902)/(-1)`

`= -6.902`

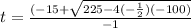
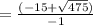
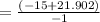
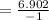
(solving b-)

`t = (-15 - √(475))/(-1)`

`= (-15-21.902)/(-1)`

`= (-36.902)/(-1)`

`= 36.902`

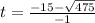
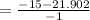
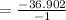
HENCE: The first solution, -6.902, is not a valid time because it is negative. The second solution, 36.902, is the time when the rocket is at a height of 100 feet. Since the rocket is at a height of more than 100 feet for the entire time after it reaches a height of 100 feet, the rocket will be at a height of more than 100 feet for 36.902 seconds.