Question

A vehicle with a mass of 2.1x10^3 kg is driving at a speed of 61 km/h around a level roadway with a curvature radius of 61 meters, just staying on the roadway (i.e., driving at the maximum safe speed for this turn and the tire treads). What is the coefficient of friction between the tires and the road? (Hint: Watch your units above.) Answer: μ = __________ (no units)

Answer 1

Given:

The mass of the vehicle is

`m=2.1*10^3\text{ kg}`

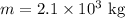
The safe speed of the vehicle is,

`v=61\text{ km/h}`

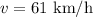
The radius of the road is,

`r=61\text{ m}`

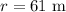
To find:

the coefficient of friction between the tires and the road

Step-by-step explanation:

For the maximum safe speed, the centripetal force is balanced by the frictional force. The frictional force is,

`F_(fr)=\mu mg`

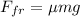
The centripetal force on the vehicle is

`F_c=(mv^2)/(r)`

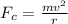
Now,

`\begin{gathered} \mu mg=(mv^2)/(r) \\ \mu=(v^2)/(gr) \end{gathered}`

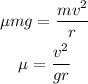
The speed is,

`\begin{gathered} v=61\text{ km/h} \\ =61*(1000)/(3600)\text{ m/s} \end{gathered}`

Now, the coefficient of friction is,

`\begin{gathered} \mu=(61*61*1000*1000)/(3600*3600*9.8*61) \\ =0.48 \end{gathered}`

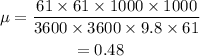
Hence, the coefficient of friction between the tires and the road is 0.48.