Given:
The mass of the vehicle is
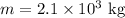
The safe speed of the vehicle is,
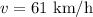
The radius of the road is,
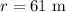
To find:
the coefficient of friction between the tires and the road
Step-by-step explanation:
For the maximum safe speed, the centripetal force is balanced by the frictional force. The frictional force is,
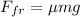
The centripetal force on the vehicle is

Now,
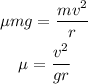
The speed is,

Now, the coefficient of friction is,
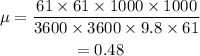
Hence, the coefficient of friction between the tires and the road is 0.48.