Question

What is the answer for this mathematical question?

Answer 1

Disagree with Chen

Explanation below

Explanation:

The vertex of a quadratic function is either the minimum or maximum of that function.

We can find the value of x for which the minimum or maximum occurs by differentiating the function with respect to x, setting the differential to 0 and solving for x.

We have

`f(x) = ax^2+bx+c = 0`

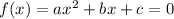
Differentiating with respect to x we get

`f'(x) = 2ax+b`

Setting this first derivative to 0 gives us

`2ax+b =0`

`2ax = -b\\`

`x = -(b)/(2a)`

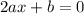
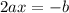
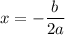
So the vertex will occur at

`x_v = -(b)/(2a)`

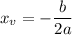
Substitute this value of
`x _v`into the original function to get the corresponding value of
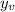`y_v` for the vertex

`f(x_v) = a\left(-(b)/(2a)\right)^2 +b\left(-(b)/(2a)\right) + c\\\\\\= a\left((b^2)/(4a^2)\right) - (b^2)/(2a) + c\\\\\\= (b^2)/(4a) -(b^2)/(2a) + c\\\\\\`

`(b^2)/(4a) -(b^2)/(2a) = -(b^2)/(4a)\\\\`

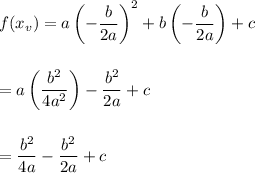
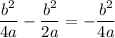
giving us

`f(x_v) = -(b^2)/(4a) + c\\\\`

The right hand side can be simplified by multiplying throughout by 4a giving

`f(x_v) = (-b^2 + 4ac)/(4a)\\\\\\`

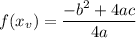
which can be re-written as

`f(x_v) = -(b^2-4ac)/(4a)`

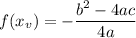
But this is nothing but the y-coordinate of the vertex ie
`y_v`

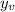
So the vertex will occur at the point

`\left(-(b)/(2a), -(b^2-4ac)/(4a)\right)`

Chen is therefore incorrect