Question

I need help with number 3 a b and c

Answer 1

(a) The minimum height happens when the value of the term cos (30t) will be equal to -1. Using special angles for cosine function, we know that -1 happens when cos x = 180. With a multiple of 30 per t minute, cos (30t) = -1 will happen at:

`\begin{gathered} 30t=180 \\ t=6 \end{gathered}`

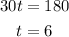
Hence, we satisfy cos (30t) = -1 at t = 6 mins. We now substitute t = 6 on the equation to solve the value of H(t), as follows:

`\begin{gathered} H(6)=12\cos (30(6))+16 \\ H(6)=12(\cos (180))+16 \\ H(6)=12(-1)+16 \\ H(6)=-12+16 \\ H(6)=4 \end{gathered}`

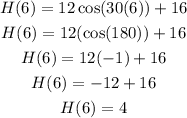
Therefore, the minimum height above the ground is 4 meters.

(b) We just substitute t = 3 on the given equation to solve for the height of the Ferris wheel after 3 minutes, as follows:

`\begin{gathered} H(3)=12\cos (30(3))+16 \\ H(3)=12(cos90)+16_{} \end{gathered}`

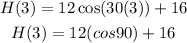
Cosine 90 is equal to zero, hence, we can simplify the equation into:

`\begin{gathered} H(3)=12(0)+16_{} \\ H(3)=16 \end{gathered}`

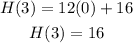
Therefore, the Ferris wheel is 16 meters above the ground after 3 minutes.

(c) One full rotation means we completed a full 360 degrees. We just need to compute for the value of t where the inside of the cosine function becomes equal to 360 degrees, as follows:

`\begin{gathered} 30t=360 \\ t=(360)/(30) \\ t=12 \end{gathered}`

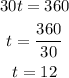
Therefore, one complete rotation happens after 12 minutes.

Answers:

(a) 4 meters

(b) 16 meters

(c) 12 minutes