(a) The minimum height happens when the value of the term cos (30t) will be equal to -1. Using special angles for cosine function, we know that -1 happens when cos x = 180. With a multiple of 30 per t minute, cos (30t) = -1 will happen at:
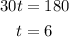
Hence, we satisfy cos (30t) = -1 at t = 6 mins. We now substitute t = 6 on the equation to solve the value of H(t), as follows:
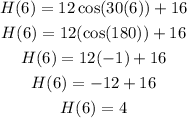
Therefore, the minimum height above the ground is 4 meters.
(b) We just substitute t = 3 on the given equation to solve for the height of the Ferris wheel after 3 minutes, as follows:
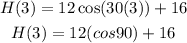
Cosine 90 is equal to zero, hence, we can simplify the equation into:
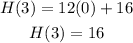
Therefore, the Ferris wheel is 16 meters above the ground after 3 minutes.
(c) One full rotation means we completed a full 360 degrees. We just need to compute for the value of t where the inside of the cosine function becomes equal to 360 degrees, as follows:
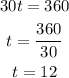
Therefore, one complete rotation happens after 12 minutes.
Answers:
(a) 4 meters
(b) 16 meters
(c) 12 minutes