Question

Question 1 Part A: (4 Points): A researcher is following the growth of a particular type of flower. She writes the given equation to show the height of the flower g(n), in inches, and n days.

Complete the inequality below by dragging and dropping the answers on the left into the given boxes

Answer 1

0 ≤ n ≤ 5

Explanation:

We have the function for growth as

`g(n) = 10(1.02)^n`

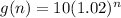
We also know that after a specific n days, the flower has grown to 11.04 inches

Since g(n) represents the height of the flower, we can substitute 11.04 for g(n) and solve for n

∴We get

`11.04 = 10(1.02)^n`

Switching sides we get

`10(1.02)^n = 11.04`

Divide both sides by 10 to get

`1.02^n = 1.104`

Take log on both sides

`\log(1.02^n) = \log(1.104)`

`\log(x^a) = a \log(x)`

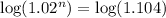
So

`\log(1.02^n) = n \log(1.02)`

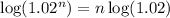
Therefore

`n \log(1.02) = \log(1.104)`

`n = (\log(1.104))/(\log(1.02))`

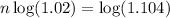
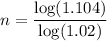
Using a calculator this works out to

`n = 4.9963`

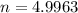
Therefore it takes at least these many days for the flower to reach 11.04 inches

Rounding number of days to 5, we get the right side of the inequality as n ≤ 5

n cannot be negative so it starts of with a value of 0 so on the right side of the inequality we get n ≥ 0 which can be rewritten as 0 ≤ n

Together the domain of n can be represented as

0 ≤ n ≤ 5

Hope that helps