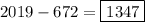Question

Find the number of positive numbers less

than 2020, which can not be written as the
sum of three consecutive positive numbers.

Answer 1

`1347`

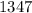
Explanation:

Let's first figure out an expression for the sum of 3 consecutive integers

If
`n` is the smallest of the 3 consecutive integers, then the next consecutive integer would be
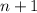`n + 1` and the next one after that,
`n + 2`

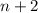
The sum of these would be

`n + (n +1) + (n +3) = 3n + 3`

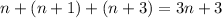
The next step is to find out many integers there are between 1 and 2019(since the question says less than 2020) that can be written as the sum of 3 consecutive integers

We get the following inequality:

`3n + 3 < 2020`

`3n = 2017`

`n = 2017/3 = 672 \textrm{ (omit fractional part)}`

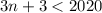
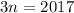
So there are 672 integers that can be expressed the sum of 3 consecutive integers

Since there are a total of 2019 integers between 1 and 2019, subtracting 672 from 2019 will give us the complement i.e. The number of positive numbers less than 2020, which cannot be written as the sum of three consecutive positive numbers.

Answer:

`2019 - 672 = \boxed{1347}`