Question

1. EF has endpoints (1,2) and (6,12). RT has endpoints (12,17) and (32,7). If EF perpendicular to RT hint: use the slope formula to calculate the slope of each segment and comare them

1. yes, the lines are perpendicular because the product of their slopes does not equal −1.
2. No, the lines are not perpendicular because the product of their slopes does not equal −1.
3. No, the lines are not perpendicular because the product of their slopes equals −1.
4. Yes, the lines are perpendicular because the product of their slopes equals −1.
2. EF has endpoints (3,7) and (13,17). RT has endpoints (4,9) and (8,5). If EF perpendicular to RT hint: use the slope formula to calculate the slope of each segment and comare them
1. No, the lines are not perpendicular because the product of their slopes does not equal −1.
2. Yes, the lines are perpendicular because the product of their slopes does not equal −1.
3. Yes, the lines are perpendicular because the product of their slopes equals −1.
4. No, the lines are not perpendicular because the product of their slopes equals −1.
3. Line m passes through points (-20,5) and (-4,7. Line n passes through points (-5,5 and 7,4 are lines m and n perpendicular? Explain Hint: Use the slope formula to calculate the slope of each segment and compare them.
1. Yes, the lines are perpendicular because the product of their slopes equals −1.
2. Yes, the lines are perpendicular because the product of their slopes does not equal −1.
3. No, the lines are not perpendicular because the product of their slopes equals −1.
4. No, the lines are not perpendicular because the product of their slopes does not equal −1.

Answer 1

option 3

Explanation:

calculate the slopes using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

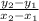
with (x₁, y₁ ) = E (1, 2 ) and (x₂, y₂ ) = F (6, 12 )

`m_(EF)` =
`(12-2)/(6-1)` =
`(10)/(5)` = 2

repeat with (x₁, y₁ ) = R (12, 17 ) and (x₂, y₂ ) = T (32, 7 )

`m_(RT)` =
`(7-17)/(32-12)` =
`(-10)/(20)` = -
`(1)/(2)`

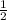
If perpendicular then the product of their slopes equals - 1

`m_(EF)` ×
`m_(RT)` = 2 × -
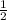`(1)/(2)` = - 1

Yes, the lines are perpendicular because the product of their slopes equal - 1

(2)

E (3, 7 ) and F (13, 17 )

`m_(EF)` =
`(17-7)/(13-3)` =
`(10)/(10)` = 1

R (4, 9 ) and T (8, 5 )

`m_(RT)` =
`(5-9)/(8-4)` =
`(-4)/(4)` = - 1

`m_(EF)` ×
`m_(RT)` = 1 × - 1 = - 1

yes, the lines are perpendicular because the product of their slopes equal - 1

(3)

(- 20, 5 ) and (- 4, 7 )

m =
`(7-5)/(-4-(-20))` =
`(2)/(-4+20)` =
`(2)/(16)` =
`(1)/(8)`

(- 5, 5 ) and (7, 4 )

m =
`(4-5)/(7-(-5))` =
`(-1)/(7+5)` = -
`(1)/(12)`

`(1)/(8)` × -
`(1)/(12)` ≠ - 1

No, the lines are not perpendicular because the product of their slopes does not equal - 1