Question

Please help me, asap!
Find f+g, f-g, fog and f/g. Determine the domain of each combination. ​

Answer 1

`\begin{aligned} \textsf{1.} \quad f + g& = 5x + 2\\f - g& = x - 4\\f \circ g &= 6x + 8\\(f)/(g)&=(3x-1)/(2x+3)\end{aligned}`

`\begin{aligned}\textsf{2.} \quad f+g&=5x-12\\f-g&=-3x+2\\f \circ g&=4x-12\\(f)/(g)&=(x-5)/(4x-7)\end{aligned}`

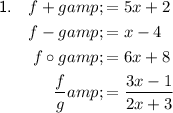
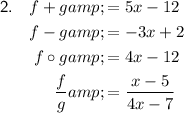
Explanation:

The domain of a function is the set of all possible input values (x-values).

Function composition is an operation that takes two functions and produces a third function.

Therefore:

• f + g means to add function f(x) to function g(x).
• f - g means to subtract function g(x) from function f(x).
• f o g means to substitute the function g(x) in place of the x in function f(x).
• f/g means to divide function f(x) by function g(x).

Question 1

Given functions:

`\begin{cases}f(x)=3x-1\\g(x)=2x+3\end{cases}`

`\begin{aligned} \implies f+g&=f(x)+g(x)\\&=(3x-1)+(2x+3)\\&=3x-1+2x+3\\&=3x+2x+3-1\\&=5x+2\end{aligned}`

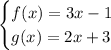
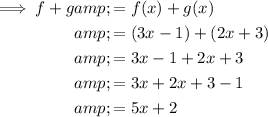
Domain of f + g: (-∞, ∞)

`\begin{aligned} \implies f-g&=f(x)-g(x)\\&=(3x-1)-(2x+3)\\&=3x-1-2x-3\\&=3x-2x-1-3\\&=x-4\end{aligned}`

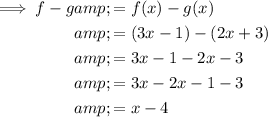
Domain of f - g: (-∞, ∞)

`\begin{aligned} \implies f \circ g&=f[g(x)]\\&=3[g(x)]-1\\&=3(2x+3)-1\\&=6x+9-1\\&=6x+8\end{aligned}`

Domain of f o g: (-∞, ∞)

`\begin{aligned} \implies (f)/(g)&=(f(x))/(g(x))\\&=(3x-1)/(2x+3)\end{aligned}`

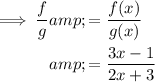
Domain of f/g: (-∞, -1.5) ∪ (-1.5, ∞)

Question 2

Given functions:

`\begin{cases}f(x)=x-5\\g(x)=4x-7\end{cases}`

`\begin{aligned}\implies f+g&=f(x)+g(x)\\&=(x-5)+(4x-7)\\&=x-5+4x-7\\&=x+4x-5-7\\&=5x-12\\\end{aligned}`

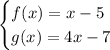
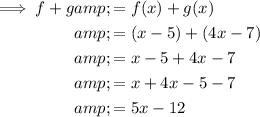
Domain of f + g: (-∞, ∞)

`\begin{aligned}\implies f-g&=f(x)-g(x)\\&=(x-5)-(4x-7)\\&=x-5-4x+7\\&=x-4x+7-5\\&=-3x+2\\\end{aligned}`

Domain of f - g: (-∞, ∞)

`\begin{aligned}\implies f \circ g&=f[g(x)]\\&=g(x)-5\\&=(4x-7)-5\\&=4x-7-5\\&=4x-12\end{aligned}`

Domain of f o g: (-∞, ∞)

`\begin{aligned}\implies (f)/(g)&=(f(x))/(g(x))\\&=(x-5)/(4x-7)\end{aligned}`

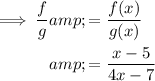
Domain of f/g: (-∞, ⁷/₄) ∪ (⁷/₄, ∞)