Step 1: Write out the formula for finding the z-score of a number
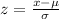

Step 2: Find the z-score of 29
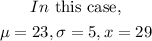
Therefore,
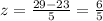
Step 3: Find a score on Exam B that has a z-score 6/5
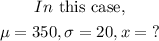
Therefore,
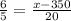
Cross-multiplying we have
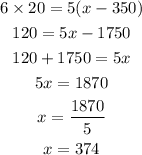
Hence, Sofia must score 374 marks in Exam B in order to do equivalently well as she did on Exam A