Question

Find Any value of c for which the system has exactly one solution. Then solve the system using the value of c that you chose. Explain each step of your solution.

y=-x-4
3y = cx-19

Answer 1

c = 4

Explanation:

Given system of linear equations:

`\begin{cases}y=-x-4\\3y=cx-19\end{cases}`

A system of linear equations will have infinite solutions if the two equations are equivalent.

A system of linear equations will have no solutions if the two equations have the same slope (i.e. parallel lines).

A system of linear equations will have one solution if the equations are different, yet the substitution of the same x-value yields the same y-value in both equations.

Rewrite the second equation to isolate y:

`\implies y=(c)/(3)x-(19)/(3)`

Therefore, the y-intercept of the first equation is -4 and the y-intercept of the second equation is -19/3.

No value of "c" can make the second equation equivalent to the first equation since the y-intercepts are different.

To find the value of "c" where there are no solutions, equate the slopes of both equations and solve for c:

`\implies (c)/(3)=-1`

`\implies c=-3`

Therefore, if c = -3, the slopes of the two lines will be the same and there will be no solutions. So "c" cannot equal -3.

Therefore, for there to be exactly one solution for the given system of linear equations, "c" can be any value except -3.

Let's choose c = 4 as an example.

Therefore:

`\begin{cases}y=-x-4\\3y=4x-19\end{cases}`

Substitute the first equation into the second equation and solve for x:

`\implies 3(-x-4)=4x-19`

`\implies -3x-12=4x-19`

`\implies -7x=-7`

`\implies x=1`

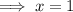
Substitute x = 1 into the first equation and solve for y:

`\implies y=-1-4`

`\implies y=-5`

Therefore, the solution to the given system of equations when c = 4 is:

• (1, -5)

Check by inputting x = 1 into both equations and comparing the resulting y-values:

`\textsf{Equation 1}: \quad y=-1-4=-5`

`\textsf{Equation 2}: \quad 3y=4(1)-19=-15 \implies y=-5`

As both equations yield y = -5 when c = 1, this confirms that when c = 5, there is one solution to the given system of equations.