Question

Solve the equation on the interval [0,2pi)

Answer 1

`\displaystyle{ \theta = (\pi)/(6), (7\pi)/(6)}`

Explanation:

Given the equation:

`\displaystyle{1 + √(3) \tan \theta = 2}`

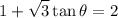
Subtract 1 both sides then divide square root of e both sides:

`\displaystyle{1 + √(3) \tan \theta - 1= 2 - 1} \\ \\ \displaystyle{ √(3) \tan \theta = 1} \\ \\ \displaystyle{\tan \theta = (1)/( √( 3) )}`

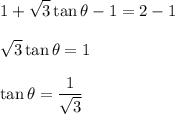
We know that tan30° or tanπ/6 is 1/√3, 30° or π/6 is a reference angle. We also have to know that tangent is positive in Q1 and its opposite (Q3). Therefore, we can find measurement in Q3 by adding π to π/6.

Q3

`\displaystyle{\pi + (\pi)/(6) = (6\pi)/(6) + (\pi)/(6)} \\ \\ \displaystyle{\pi + (\pi)/(6) = (7 \pi)/(6) }`

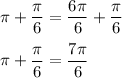
Since the interval is given from 0 to 2π (full completed rotation), therefore, only π/6 and 7π/6 are the solutions.

`\displaystyle{ \therefore \theta = (\pi)/(6), (7\pi)/(6)}`