Answer: 92
Explanation:
Observe that the probability is symmetric around
 .
.
If
 , then
, then
 . By the triangle inequality, it follows that
. By the triangle inequality, it follows that
 .
.
We can now rearrange as follows:
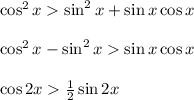
Since
 and
and
 are both positive for the chosen interval,
are both positive for the chosen interval,
 .
.
Therefore, the probability is
 .
.
This means,
 .
.